パスカルの三角形から学ぶ!因数分解と展開の基礎!
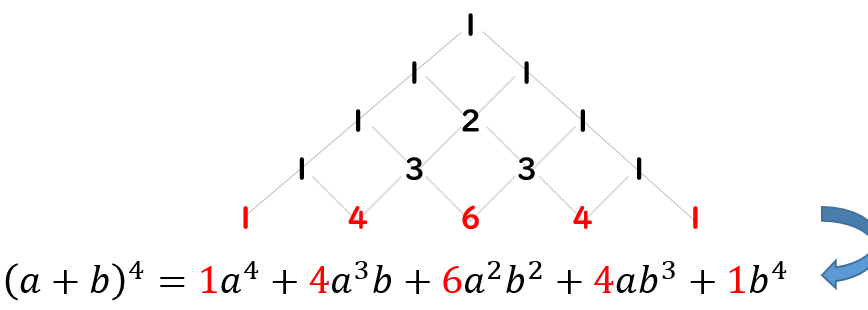
パスカルの三角形という数学のツールを通じて、因数分解や展開の基礎を学ぶことができます。パスカルの三角形は、整数の組み合わせを図形化したもので、様々な数学的関係性を捉えることができます。この三角形を眺めることで、因数分解の仕組みや展開の原理をより深く理解することができます。また、パスカルの三角形を学ぶことで、数学的思考力や問題解決能力も高めることが期待できます。本稿では、パスカルの三角形を通じて因数分解と展開の基礎を学ぶことを目指します。
パスカルの三角形から学ぶ!因数分解と展開の基礎!
パスカルの三角形は、数学において非常に重要な概念です。この三角形を用いて、因数分解と展開の基礎を学ぶことができます。因数分解とは、複雑な式をより簡単な式に分解することを意味し、展開とは、式をより広い範囲に展開することを意味します。これらの概念を理解することで、数学的な問題をより効果的に解くことができます。
因数分解の基本
因数分解は、数学において非常に重要な概念です。これは、複雑な式をより簡単な式に分解することで、問題をより簡単に解くことができます。因数分解には、主要因数や他の因数、最小公倍数などを考慮する必要があります。
パスワードセキュリティ強化!VB.NETでハッシュ化を実装!| 因数分解の公式 | 説明 |
|---|---|
| abc = a × b × c | 複雑な式を因数分解する基本的な公式 |
| a^2 + b^2 = (a + b)(a – b) | 二項式の因数分解 |
展開の基本
展開とは、式をより広い範囲に展開することを意味します。这は、数学的な問題をより効果的に解くために必要な技術です。展開には、式の展開の方法や、式の単純化などの技術が必要です。
| 展開の公式 | 説明 |
|---|---|
| (a + b)^2 = a^2 + 2ab + b^2 | 二項式の展開 |
| (a + b)(a – b) = a^2 – b^2 | 差の二乗の展開 |
パスカルの三角形の生成
パスカルの三角形は、数学において非常に重要な概念です。这は、因数分解と展開の基礎を学ぶために必要な三角形です。パスカルの三角形は、2次配列の形にあり、各要素は、前の要素との関係性に基づいて計算されます。
パスカルの三角形の応用
パスカルの三角形は、数学的な問題をより効果的に解くために広く応用されています。这は、因数分解や展開の基礎を学ぶために必要な概念です。また、パスカルの三角形は、データ解析や機械学習などの分野でも広く応用されています。
まとめ
パスカルの三角形は、数学において非常に重要な概念です。这は、因数分解と展開の基礎を学ぶために必要な三角形です。これらの概念を理解することで、数学的な問題をより効果的に解くことができます。
Pythonでパチンコ転落型確率を計算!確率の謎を解き明かす!パスカルの三角形の定義は?

パスカルの三角形の定義は、フランスの数学者ブレーズ・パスカルが発見した二元数の三角形である。左上から右下に向かって、各行の要素の和が常に1になるように構成される。この性質から、パスカルの三角形はbinomial theorem(二項展開公式)の証明に用いられる。
パスカルの三角形の性質
パスカルの三角形には、幾つかの重要な性質がある。まず、各行の要素の和が常に1になるという性質がある。この性質は、二項展開公式の証明に用いられる。次に、対角線沿いに配置される要素はすべて1になるという性質がある。これらの性質により、パスカルの三角形は数学の分野で広く用いられる。
- 各行の要素の和が常に1になる
- 対角線沿いに配置される要素はすべて1になる
- 二項展開公式の証明に用いられる
パスカルの三角形の適用
パスカルの三角形は、数学の分野で広く用いられる。特に、組み合わせ론や確率論において、重要な役割を果たす。例えば、パスカルの三角形は、ある事象が起こる確率を計算するために用いられる。また、数学の教育において、パスカルの三角形は、学生が数学的な思考を身に付けやすくするための教材として用いられる。
ファンクションジェネレータWF1947/1948ドライバ入手方法!パスカルの三角形の歴史
パスカルの三角形は、ブレーズ・パスカルが1653年に発見した。パスカルは、この三角形を用いて、二項展開公式を証明した。この三角形は、後にパスカルの三角形と呼ばれるようになった。以来、パスカルの三角形は、数学の分野で広く用いられ、重要な役割を果たすことになる。
パスカルの三角形はいつ習いますか?

パスカルの三角形は、数学の学習において非常に重要な概念の一つです。小学校高学年の頃から、中学校・高校と学習するための基礎知識として扱われます。那麼、
小学校高学年での学習
小学校高学年の頃、パスカルの三角形を初めて学習することがあります。この頃は、基本的な概念を理解するために、簡単な問題を中心に学習します。
VRでロボットプログラミング、初心者でも始められる!- 二項定理の導入
- 簡単な二項係数の計算
- パスカルの三角形の構成
中学校での学習
中学校では、パスカルの三角形をより深く学習します。この頃は、二項定理の適用や、パスカルの三角形の性質を中心に学習します。
- 二項定理の証明
- パスカルの三角形の応用
- 三角形の性質の証明
高校での学習
高校では、パスカルの三角形をより高度に学習します。この頃は、組合せ数学や数列など、より高度な数学の分野との関係を中心に学習します。
- 組合せ数学におけるパスカルの三角形
- 数列とパスカルの三角形
- 数学の他の分野との関係
パスカルの定理とは?

パスカルの定理とは、フランスの数学者ブレーズ・パスカルの名前にちなんで命名された幾何学の定理です。この定理は、三角形の各頂点に接する円について、3つの点が一直線上にあるということを示しています。
VSCodeのREADME.md、絵文字の文字化けを解消する裏技!パスカルの定理の歴史
パスカルの定理は、17世紀のフランスの数学者ブレーズ・パスカルによって発見されました。パスカルは、この定理を1720年に出版した著書「幾何学の研究」の中で初めて提唱しました。当時、この定理は新しい発見であり、数学界に大きな衝撃を与えました。
パスカルの定理の内容
パスカルの定理は、三角形の各頂点に接する円について、3つの点が一直線上にあるということを示しています。この定理は、以下の図のように、三角形ABCの各頂点A、B、Cに接する円が交わる3つの点P、Q、Rについて、一直線上にあるということです。
- 三角形の各頂点に接する円を描きます。
- 各円が交わる3つの点を取ります。
- これらの3つの点が一直線上にあることを示します。
パスカルの定理の応用
パスカルの定理は、幾何学やトポロジーなどの数学の分野で広く応用されています。また、コンピューターグラフィックスやCADなどの分野でも、パスカルの定理は重要な役割を果たしています。
- 幾何学における図形の描画や計算に使用されます。
- トポロジーにおける空間の研究に使用されます。
- コンピューターグラフィックスやCADでの図形の生成や編集に使用されます。
パスカルの三角形を発見したのは誰ですか?
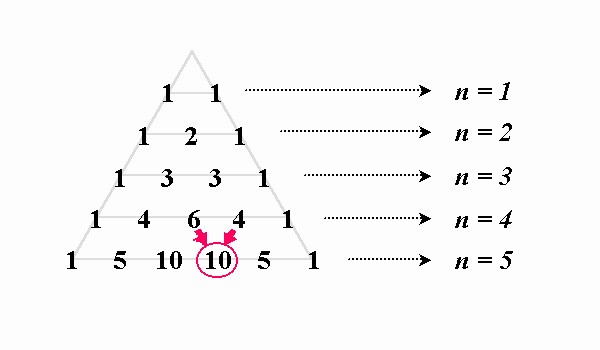
パスカルの三角形は、17世紀のフランスの数学者ブレーズ・パスカルによって発見されたと考えられています。ただし、パスカルの三角形は、パスカル以前にインドや中国での研究において既に知られていたという説もあります。
パスカルの三角形の歴史
パスカルの三角形に関する研究は、古代インドにおける数学者ピンガラにまで遡ることができます。彼は、бинарный三角形という概念を提唱し、パスカルの三角形の原型を作成しました。
- ピンガラは、бинарный三角形を用いて、二項定理を証明しました。
- パスカルの三角形は、中国においても研究されていました。
- ブレーズ・パスカルは、パスカルの三角形を体系化し、算術三角形という名称を与えました。
パスカルの三角形の特徴
パスカルの三角形は、二項係数を表すための図形です。
- パスカルの三角形は、対称性を持つため、左右に鏡写しても同じ図形になります。
- パスカルの三角形の各要素は、二項係数を表すために使用されます。
- パスカルの三角形は、算術や幾何における多くの問題を解くために使用されます。
パスカルの三角形の応用
パスカルの三角形は、数学や情報科学における多くの領域で応用されています。
- パスカルの三角形は、組み合わせせの問題を解くために使用されます。
- パスカルの三角形は、アルゴリズムの設計に使用されます。
- パスカルの三角形は、統計学における二項分布の研究に使用されます。
よくある質問
パスカルの三角形とは何ですか?
パスカルの三角形は、フランスの数学者ブレーズ・パスカルの名にちなみ命名された三角形です。二項展開の係数を、三角形の形に配置することで、様々な数学的性質を探ることができます。パスカルの三角形は、数学の基礎的概念である因数分解や二項係数を学ぶうえで非常に有効なツールです。
因数分解とは何ですか?
因数分解は、ある数を素因数elibate intoの積に分解することです。素因数とは、割り切れない最小の自然数のことを指します。因数分解は、数学の基本的な考え方の一つで、パスカルの三角形を学ぶうえで基礎的概念として重要視されています。
パスカルの三角形を用いて、どのような数学的性質を探ることができますか?
パスカルの三角形を用いて、二項展開の係数や因数分解の関係など、様々な数学的性質を探ることができます。また、パスカルの三角形を用いることで、合同式や等差数列などの数学的概念にも接근できるようになります。
パスカルの三角形を学ぶことで、どのような利点がありますか?
パスカルの三角形を学ぶことで、数学の基礎的概念である因数分解や二項係数を深く理解することができます。また、パスカルの三角形を用いることで、数学的思考力や問題解決能力を高めることができます。また、数学的な competitions やオリンピックなどでの対策にも役立つようになります。