ハノイの塔に挑戦!C#で再帰アルゴリズムを実装!
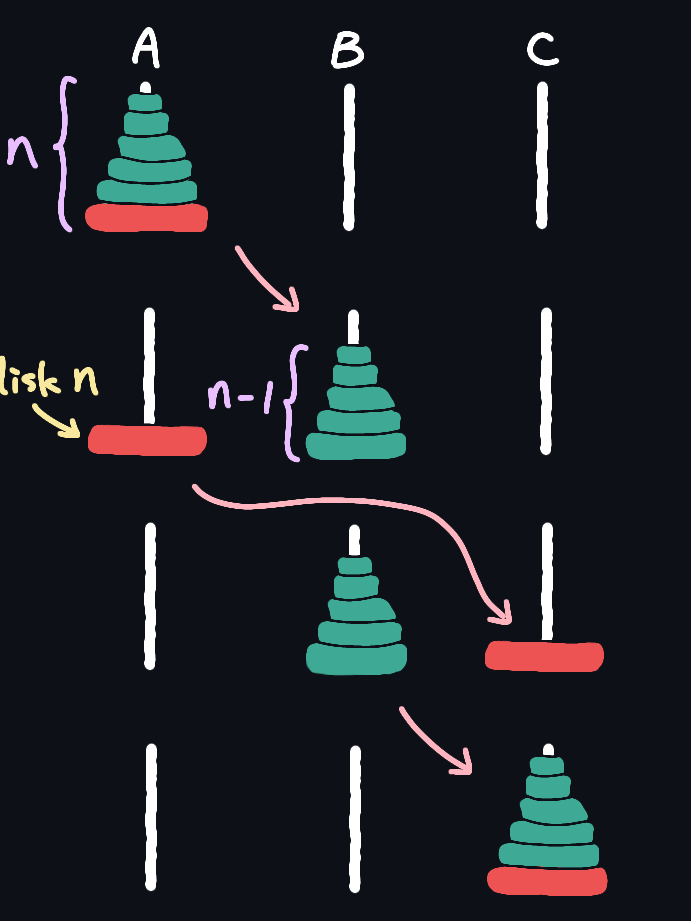
ハノイの塔は古代インドの数学者が考案したとされるパズルであり、世界中で広く知られている。プログラムでハノイの塔を解くには、再帰アルゴリズムを使用することが有効である。今回はCを使用してハノイの塔を再帰アルゴリズムで解いていく。ハノイの塔を解くためのアルゴリズムを実際に作成し、Cでの実装方法を解説していくことで、再帰アルゴリズムの理解を深めることができる。
ハノイの塔に挑戦!Cで再帰アルゴリズムを実装!
ハノイの塔は、古くから知られるパズルゲームです。このゲームでは、三本の棒に Kommentar 個の円盤を移動する必要があります。最上段には一番小さい円盤が、最下段には一番大きい円盤があり、円盤を移動する際には、常に上に置く円盤は下にある円盤よりも小さくなければならないというルールがあるため、非常に困難なパズルゲームとなっています。
ハノイの塔のルール
ハノイの塔のゲームでは、次のようなルールがあります。三本の棒があり、円盤を移動する必要があります。最上段には一番小さい円盤が、最下段には一番大きい円盤があり、円盤を移動する際には、常に上に置く円盤は下にある円盤よりも小さくなければならないというルールがあるため、非常に困難なパズルゲームとなっています。
バイナリ形式VTKファイル出力方法!実践的なコード例付き!再帰アルゴリズムの導入
ハノイの塔を解くために、再帰アルゴリズムを使用することができます。再帰アルゴリズムとは、自分自身を呼び出す関数のことです。このアルゴリズムを使用することで、非常に大きな円盤も移動することができます。
Cでの実装
Cでは、ハノイの塔を実装するために、次のようなコードを使用することができます。 public static void Hanoi(int n, char from, char to, char via) { if (n == 1) { Console.WriteLine(Move disk 1 from + from + to + to); } else { Hanoi(n – 1, from, via, to); Console.WriteLine(Move disk + n + from + from + to + to); Hanoi(n – 1, via, to, from); } } このコードでは、再帰関数を使用して、ハノイの塔を解いています。
アルゴリズムの分析
ハノイの塔のアルゴリズムを分析すると、時間計算量はO(2^n)となっています。また、空間計算量はO(n)となっています。これらの計算量が非常に大きなため、非常に大きな円盤を移動するには、非常に長い時間がかかることになります。
ハノイの塔の応用
ハノイの塔は、データ構造やアルゴリズムを学ぶための非常に有効な例です。また、問題解決能力を高めるためのトレーニングにも非常に適しています。
バッチ画像処理を効率化!Python GUIフレームワーク徹底比較!| 円盤の個数 | 時間計算量 | 空間計算量 |
|---|---|---|
| 1 | O(1) | O(1) |
| 2 | O(2) | O(2) |
| 3 | O(4) | O(3) |
| 4 | O(8) | O(4) |
| 5 | O(16) | O(5) |
ハノイの塔 何年かかる?

ハノイの塔は、3つの円盤を移動するパズルゲームで、最小の手数で解くことが目標です。ゲームの難易度は、円盤の数によって異なります。3つの円盤の場合、最少7手で解くことができます。但し、円盤の数が増加すると、ゲームの難易度も増加し、手数も増加します。
ハノイの塔の歴史
ハノイの塔は、1883年にフランスの数学者エドゥアール・ルーカスによって創造されたゲームです。ルーカスは、このゲームを「Tower of Hanoi」と名付けました。当初は、数学の教育用に作られたゲームでしたが、現在では世界中で広く知られており、パズルゲームのクラシックとなっています。
- 1883年:エドゥアール・ルーカスがハノイの塔を創造
- 20世紀:ハノイの塔が世界中で広く知られるようになる
- 現在:ハノイの塔はパズルゲームのクラシックとなっています
ハノイの塔の解き方
ハノイの塔を解くには、規則を覚えておく必要があります。基本的な規則は、上に小さい円盤を置くということです。また、一つのピラーに同じ大きさの円盤を置くことはできません。これらの規則を踏み、円盤を移動することで、ゲームを解くことができます。
バーサライタ(POV)自作ガイド!作り方と注意点を紹介!- 上に小さい円盤を置く
- 一つのピラーに同じ大きさの円盤を置かない
- 円盤を移動してゲームを解く
ハノイの塔の数学的側面
ハノイの塔は、数学的側面でも非常に重要なゲームです。再帰反復という数学的概念を学ぶことができます。ゲームの解き方は、再帰反復の考え方を適用することで、最少の手数で解くことができます。また、ゲームの難易度は、円盤の数によって異なりますが、数学的には指数関数的に増加します。
- 再帰反復の数学的概念を学ぶ
- ゲームの解き方に再帰反復を適用する
- 円盤の数によってゲームの難易度が指数関数的に増加する
ハノイの塔の構造は?
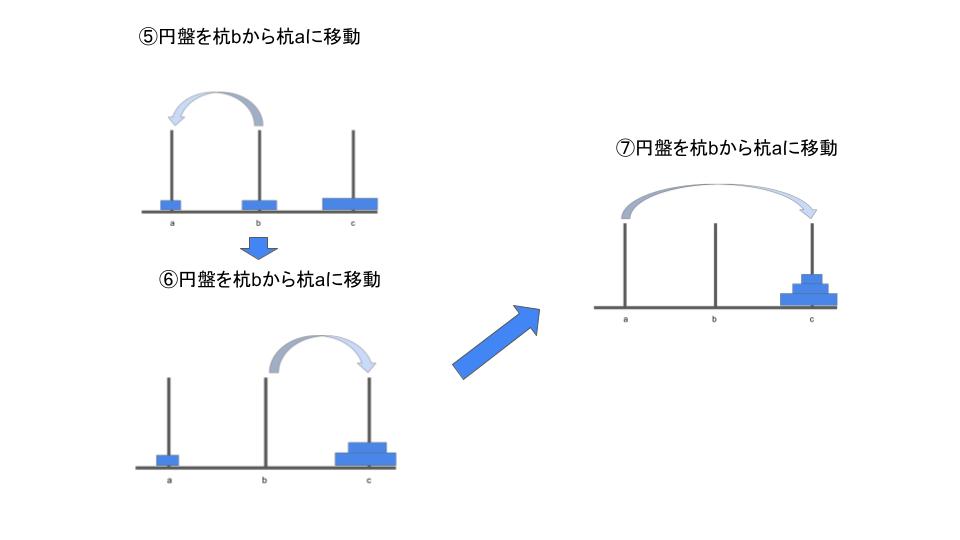
ハノイの塔の構造は、数学の基礎に基づいて設計されています。塔の構造は、3つの柱に分けられており、それぞれの上には片方の盤が乗っています。盤の大きさは、下から上に向かって小さくなっています。
ハノイの塔の基本的なルール
ハノイの塔の게임をプレイするためには、次のルールを遵守する必要があります。
パスカルの三角形から学ぶ!因数分解と展開の基礎!- 上にある盤は、下にある盤よりも小さくてなければならない。
- 盤を移動するときは、柱の上にある盤ひとつだけを移動させることができる。
- 移動した盤は、他の柱の上にある盤の上にしか置くことができない。
ハノイの塔の目的
ハノイの塔の目的は、初めの状態から最終的な状態にすることです。つまり、A柱にあり初めの状態にある盤を、C柱にすべて移すことができるようにすることです。
ハノイの塔の解き方
ハノイの塔を解くためには、再帰的手法を使用することができます。まず、最上位の盤を移動させるために、下にある盤を移動させる必要があります。次に、下にある盤を移動させるために、更に下にある盤を移動させる必要があります。このように、再帰的に盤を移動させて、最終的に目的の状態にすることができます。
- 最上位の盤を移動させる。
- 下にある盤を移動させる。
- 更に下にある盤を移動させる。
よくある質問
ハノイの塔のアルゴリズムは何ですか?
ハノイの塔のアルゴリズムは、再帰という手法を用いて盤面上の円盤を移動するものです。これにより、最小の移動回数で円盤を移動することができます。具体的には、最上段の円盤を移動するためにはその下にある円盤を移動する必要があり、それを繰り返すことで円盤を移動することができます。このアルゴリズムを用いることで、ハノイの塔のゲームを効率的にクリアすることができます。
Cでハノイの塔を実装するОпてもっとも適切な方法は何ですか?
Cでハノイの塔を実装する場合、再帰関数を用いることがもっとも適切です。これは、Cがサポートしている言語機能であり、ハノイの塔のアルゴリズムに適切にマッチングします。再帰関数を用いることで、簡潔にハノイの塔を実装することができます。また、Cのリストを用いることで円盤の状態を管理することもできます。
パスワードセキュリティ強化!VB.NETでハッシュ化を実装!ハノイの塔のゲームの LT とは何ですか?
ハノイの塔のゲームの LT とは、最小の移動回数で円盤を移動することを指します。これを実現するためには、ハノイの塔のアルゴリズムを用いる必要があります。このアルゴリズムを用いることで、円盤を最小の移動回数で移動することができます。具体的には、再帰を用いて円盤を移動することで LT を実現することができます。
ハノイの塔のゲームをクリアするためには何回の移動が必要ですか?
ハノイの塔のゲームをクリアするためには、2のn乗 – 1回の移動が必要です。nは円盤の数を示しています。これは、ハノイの塔のアルゴリズムに基づいて計算される値であり、最小の移動回数で円盤を移動することを保証します。具体的には、再帰を用いて円盤を移動することで、この移動回数を実現することができます。