最小二乗法とは？ 線形回帰分析での推定方法をわかりやすく解説！

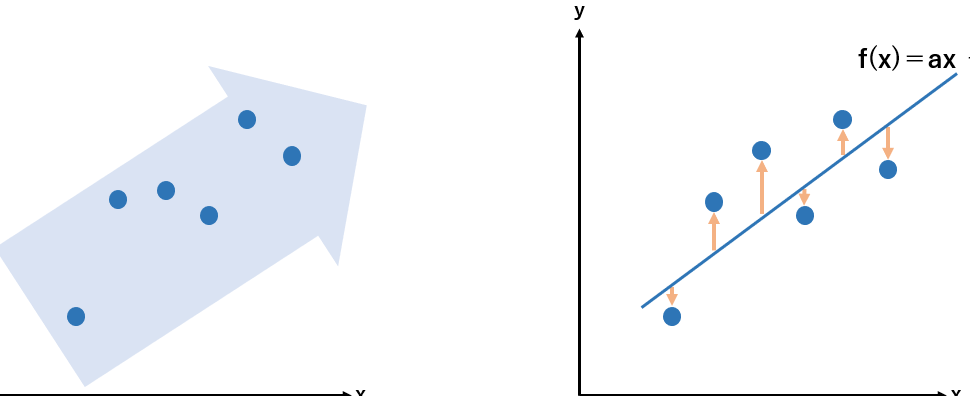
線形回帰分析において、最小二乗法という手法が頻繁に用いられます。この手法は、データから目的変数と説明変数の関係を推定するために利用され、統計モデルの構築や予測精度の高めるために不可欠なツールとなっています。しかし、最小二乗法の理論的な背景や、実際の分析での適用方法について、わかりやすく説明される機会は少ないと言えます。本稿では、最小二乗法の概要や、線形回帰分析での推定方法をわかりやすく解説し、読者の理解を深めることを目指します。

最小二乗法の基礎知識：線形回帰分析での重要な推定方法

最小二乗法とは、線形回帰分析において、目的変数と説明変数の関係を最小限度に残差を小さくするための推定方法のことです。この方法は、多くのフィールドで広く使われており、統計解析、機械学習、経済学などに応用されています。

最小二乗法の原理

最小二乗法の原理は、残差平方和を最小化することを目的としています。この目的達成のために、最小二乗法では、説明変数の係数を推定し、目的変数と説明変数の関係をモデル化します。

最小二乗法の種類

最小二乗法には、2つの主要な種類があります。1つは、普通最小二乗法、もう1つは、重み付き最小二乗法です。普通最小二乗法は、全てのデータポイントに同じ重みを与えることで、残差平方和を最小化します。一方、重み付き最小二乗法は、各データポイントに異なる重みを与えることで、特定のデータポイントに重点を置くことができます。

最小二乗法の利点

最小二乗法の利点は、以下の4点です。 簡単: 最小二乗法は、他の統計手法に比べて、簡単に実施することができます。 汎用性: 最小二乗法は、多くのフィールドで応用することができます。 高度な精度: 最小二乗法は、高度な精度で推定結果を得ることができます。 計算速度: 最小二乗法は、高速に計算を行うことができます。

最小二乗法の限界

最小二乗法には、以下の3点の限界があります。 非線形関係: 最小二乗法は、非線形関係には適用できません。 多重共線性: 最小二乗法は、多重共線性の問題に弱いです。 外れ値: 最小二乗法は、外れ値の影響を受けやすいです。

最小二乗法の実際の例

最小二乗法を実際に適用する例として、株式価格予測や、顧客の購入 hànhviourの分析などがあります。例えば、株式価格予測においては、株式の過去の価格や経済指標を説明変数として、将来の株式価格を目的変数として、最小二乗法を適用することができます。

回帰分析における最小二乗法とは？

回帰分析における最小二乗法とは、統計学において、観測されたデータに基づいて、最小二乗,errorを最小化するように、回帰式の係数を推定する手法です。

最小二乗法の特徴

最小二乗法は、以下の特徴を持っています。

1. 線形回帰分析でのみ適用可能
2. 最小二乗を最小化することで、推定される係数が観測されたデータに最も近い値を示す
3. 正規分布に従う誤差項を仮定する必要がある

最小二乗法のメリット

最小二乗法には、以下のメリットがあります。

1. 簡単に計算可能
2. 計算結果が一意である
3. ,errorの影響を最小限りに留めることができる

最小二乗法の適用例

最小二乗法は、以下のような場合に適用されます。

1. 経済指標の予測
2. 科学研究での実験結果の分析
3. マーケティングでの消費者行動の分析

最小二乗法とはどのような解析手法ですか？

最小二乗法とは、itori ōkā hō（ordinary least squares）とも呼ばれる統計学的解析手法の一種です。この方法は、データ間に含まれるノイズや誤差を最小化することで、実際の関係をより正確に捉えることを目指しています。

最小二乗法の原理

最小二乗法は、最小二乗原理に基づいています。この原理は、データ間に含まれるノイズや誤差を最小化することで、実際の関係をより正確に捉えることを目指しています。この原理に基づいて、最小二乗法は、データの線形近似を行い、実際の関係を捉えることを目指しています。

1. データの線形近似を行うことで、実際の関係を捉えることができます。
2. 最小二乗原理に基づいて、ノイズや誤差を最小化することができます。
3. 実際の関係を捉えるために、データの線形近似を行う必要があります。

最小二乗法の特徴

最小二乗法には、線形独立や等分散の仮定が含まれています。これらの仮定に基づいて、最小二乗法は、データの回帰分析を行うことができます。また、最小二乗法は、パラメーターの推定を行うことができます。

1. 線形独立の仮定に基づいて、データの回帰分析を行うことができます。
2. 等分散の仮定に基づいて、パラメーターの推定を行うことができます。
3. 最小二乗法は、パラメーターの推定を行うことができます。

最小二乗法の応用

最小二乗法は、統計学、経済学、工学等の分野で広く応用されています。また、最小二乗法は、予測や分析のために使用されます。

1. 統計学での応用：最小二乗法は、統計学でのデータ分析に広く応用されています。
2. 経済学での応用：最小二乗法は、経済学での予測や分析に広く応用されています。
3. 工学での応用：最小二乗法は、工学での予測や分析に広く応用されています。

最小二乗法とはITで何ですか？

最小二乗法とは、観測されたデータに基づいて、どのくらいの誤差があるかを計算するための統計的手法です。

最小二乗法の基本的な考え方

最小二乗法は、観測されたデータと理論的なモデルとの誤差を最小化することを目指しています。最小二乗という名前は、この手法が誤差の二乗を最小化することを示しています。具体的には、データとモデルとの差分を二乗し、その和を最小化することで、最適なパラメーターの値を推定しています。

最小二乗法の利点

最小二乗法には、以下のような利点があります。

1. 簡単に計算できるため、実際のデータ分析に適しています。
2. 誤差の進行方向を把握できるため、モデルを改良するための指標となります。
3. 多くの統計ソフトウェアが対応しているため、容易に実装できます。

最小二乗法の応用例

最小二乗法は、多くの分野で応用されています。

1. 経済の予測モデルでは、経済指標と予測モデルとの誤差を最小化するために使用されます。
2. 機械学習では、誤差を最小化することで、最適なパラメーターの値を推定しています。
3. 科学研究では、実験結果と理論との誤差を最小化するために使用されます。

最小二乗基準円とは？

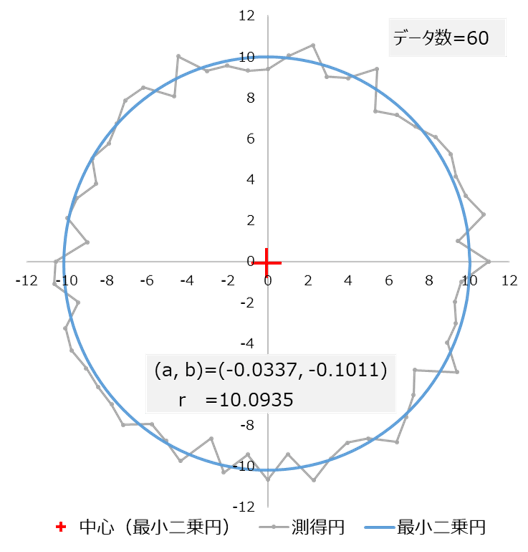
最小二乗基準円（せいしよじょうきじゅんえん）は、統計学における回帰分析の一種で、独立変数と従属変数の関係を最小二乗法によって推定するための基準円のことである。最小二乗法は、観測データにおける誤差の二乗和を最小にするように、回帰曲線を決定する手法である。

最小二乗基準円の特徴

最小二乗基準円には、以下のような特徴がある。

1. 最小二乗法を用いるため、誤差の二乗和を最小にするように回帰曲線を決定する。
2. 独立変数と従属変数の関係を線形や非線形の形で捉えることができる。
3. 基準円の中心を原点に設定することで、独立変数の効果を測ることができる。

最小二乗基準円の利点

最小二乗基準円には、以下のような利点がある。

1. 簡単な計算：最小二乗法を用いるため、計算が簡単に行える。
2. 高精度：誤差の二乗和を最小にするように回帰曲線を決定するため、高精度の結果を得ることができる。
3. 汎用的適用：独立変数と従属変数の関係を線形や非線形の形で捉えることができるため、様々な分野での適用が可能である。

最小二乗基準円の注意点

最小二乗基準円には、以下のような注意点がある。

1. 前提条件：独立変数と従属変数が線形の関係にあることを前提としているため、非線形の関係にある場合は適さない。
2. 外れ値の影響：外れ値の存在によって、結果が大きく変化することがある。
3. 過学習の問題：独立変数の数が多い場合、過学習によって結果が不正確になることがある。

よくある質問

最小二乗法とは何か：

最小二乗法は、線形回帰分析のための推定方法の一つです。この方法では、観測データに対して、最小二乗原理に基づいて回帰式を推定します。具体的には、独立変数と従属変数の関係を表す回帰係数を推定し、予測や解析に役立つ値を導き出します。

最小二乗法の目的は何ですか：

最小二乗法の目的は、線形関係にある独立変数と従属変数の間に、最適な回帰式を探索することです。この方法を用いることで、予測精度を高めることができ、統計モデルの評価にも役立つ値を提供します。また、最小二乗法を用いることで、因果関係の解析や予測モデルの構築にも貢献します。

最小二乗法の計算方法は何ですか：

最小二乗法の計算方法は、普通の最小二乗法と重み付き最小二乗法の2種類があります。普通の最小二乗法では、観測データに対して均方誤差を最小化するために、回帰係数を推定します。一方、重み付き最小二乗法では、観測データに対する重みを設定し、回帰係数を推定します。これにより、観測誤差や重みの影響を調整することができます。

最小二乗法の利点は何ですか：

最小二乗法の利点は、簡単に計算できること、広範囲の適用が可能であること、統計的妥当性が高いため信頼性が高いことなど多岐にわたります。また、最小二乗法を用いることで、予測モデルの構築や因果関係の解析に役立つ情報を得ることができます。

レン、「技術分野における最高のガイド」の創設者です。

私は職業としてのエンジニアではありませんが、情熱としてのエンジニアです。技術分野における最高のガイドを立ち上げたのは、デジタル世界のあらゆる知識やリソースを紹介するためです。すべてをよりシンプルで理解しやすい視点から誰にでも伝えられるよう心がけています。