その分数は本当に整数と等価? 判別方法を解説!

整数という概念は、数学の基礎にあるものですが、その分数が本当に整数と等価であるかは、数学の初歩を学んでいる者でも理解しづらい場合があります。例えば、1÷2=0.5という結果になるが、この0.5が整数と等価であるということは本当でしょうか。数学の公式や計算に基づいて、その分数が整数と等価であるかどうかを判別する方法があります。本稿では、その判別方法をわかりやすく解説し、数学の初歩を学んでいる者にとって参考になる内容を提供します。
その分数は本当に整数と等価? 判別方法を解説!
その分数は、整数と等価かどうかを判別することは、数学の基本的な問題の一つです。しかし、この問題に対する回答は、非常に簡単ではありません。なぜなら、分数と整数は、異なる数値体系に属するためです。この記事では、分数と整数の等価性を判別するための方法を、詳しく解説します。
分数とは何か?
分数は、しばしば、割合や率を表すための数値体系です。分母と分子の組み合わせによって、分数の値を表現します。例えば、1/2や3/4のように、分数は、整数の割合を表すために用いられます。
大規模アジャイルフレームワーク、本当に必要? そのメリット・デメリット整数とは何か?
整数は、正の整数や負の整数を含む、有限の整数値の範囲を指します。整数は、分数とは異なる数値体系に属し、有限の値を表現します。例えば、1や-1のように、整数は、有限の個数を表すために用いられます。
分数と整数の等価性を判別する方法
分数と整数の等価性を判別するためには、分数を分母と分子に分解し、分母が1になれば、整数と等価であることがわかります。例えば、2/2や3/3のように、分母が1の分数は、整数と等価です。
| 分数 | 整数 |
|---|---|
| 2/2 | 1 |
| 3/3 | 1 |
| 1/2 | ≠整数 |
| 3/4 | ≠整数 |
分数の性質
分数には、有理数や無理数などの性質があります。有理数は、有限の小数を有する分数を指し、無理数は、無限小数を有する分数を指します。例えば、1/2は有理数、πは無理数です。
分数と整数の関係性
分数と整数は、異なる数値体系に属しますが、両者には 換算 という関係があります。換算とは、分数を整数に変換するための方法です。例えば、1/2を2と換算することができます。
なぜExcelの指数はわかりにくい? その理由を徹底解説!分数と整数を混ぜて計算するにはどうすればいいですか?

分数と整数を混ぜて計算するには、両方の数値を同じ単位に統一する必要があります。那には、二つの方法があります。
分数を整数に換算する
分数を整数に換算するには、分母を共通にする必要があります。共通分母にすることで、分数を整数に換算することができます。
- 分母を共通にすることで、分数の分母は等しくなる。
- 分数の分子を共通分母で割り、整数にする。
- 整数になった分数を計算する。
整数を分数に換算する
整数を分数に換算するには、分子に整数を乗じて、分母に1を置く必要があります。分母1にすることで、整数を分数に換算することができます。
5年経った今、なぜRustを学ぶべきなのか? 改めてまとめてみた- 整数に分子を乗じて、分数を作る。
- 分母に1を置く。
- 分数になった整数を計算する。
分数と整数の計算例
分数と整数を混ぜて計算する例えば、2 1/2と3を足す計算です。
- 分数1/2を整数3に換算する。
- 分数1/2を3/2に換算する。
- 2と3/2と3を足す。
分数は整数ですか?
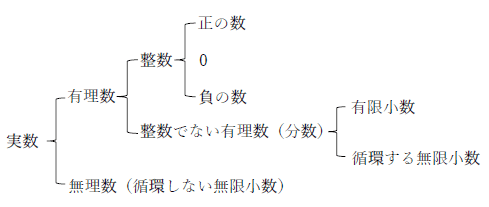
分数は、整数の一種ではありません。分数は、分子と分母からなる割合を表す数学的概念です。一方、整数は、有限個の連続する自然数のうちのある一個の値を指します。したがって、分数は整数には含まれません。
分数と整数の違い
分数と整数の主な違いは、小数点の有無です。整数には小数点が無く、有限個の数字で表されます。一方、分数には小数点が有り、有限個の数字に小数点以下の数字を追加することで表されます。
ループカウンタ変数に “i” が使われる理由:知られざる歴史とは?- 整数:例えば、1、2、3など
- 分数:例えば、1/2、3/4、2/3など
分数の表記方法
分数には、分子と分母の2つの部分があります。分子は、割合のうちの上部にある数字を指し、分母は、割合のうちの下部にある数字を指します。
- 分子:割合の上部にある数字
- 分母:割合の下部にある数字
分数の運用
分数は、算数や幾何学など、数学的計算において広く使用されます。また、料理や工学などの分野でも、分数は重要な役割を果たしています。
- 算数:分数を用いての加減乗除などの計算
- 幾何学:分数を用いての図形の計算
- 料理:分数を用いてのレシピの作成
分母と分子が整数の分数で表される数は何といいますか?
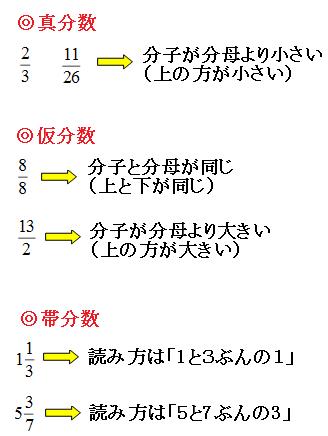
整数比と呼ばれる数です。
Arduinoライブラリ入門! 初めてでも大丈夫! 簡単ガイド整数比の定義
整数比は、分母と分子が整数である分数で表される数を指します。例えば、1/2、3/4、2/3などといった数が整数比に該当します。このような数は、有限小数や循環小数を用いて表現することができます。
整数比の例
- 1/2 = 0.5
- 3/4 = 0.75
- 2/3 = 0.666…
整数比の性質
整数比には、以下のような性質が存在します。
- 有限小数や循環小数を用いて表現することができる
- 計算結果が有限小数や循環小数になる
- 分母と分子の最小公倍数を取ることで簡約できる
よくある質問
分数が整数と等価ということ 왓시?
分数が整数と等価ということは、数学的には同値ということを指しています。つまり、分数と整数は、計算結果の上では同一の値を示すということです。しかし、この同値関係は、必ずしも分数と整数が同じ形式を持つことを意味しません。むしろ、分数と整数は異なる形式を持つが、計算結果の上では同一の値を示すという関係性を指しています。
整数と等価な分数を判別するにはどのように?
分数が整数と等価かどうかを判別するためには、分数の分母が1であるかどうかを確認することができます。すなわち、分数がa/1の形であれば、整数aと等価であることがわかります。また、分数を小数に展開してみても、有限小数であり循環小数でない場合、整数と等価であると考えられます。
分数が整数と等価になる条件は?
分数が整数と等価になる条件は、分数の分母が1であることです。また、分数が有限小数であり循環小数でない場合も、整数と等価であると考えられます。つまり、分数が整数と等価になるためには、分数の形が有限な小数であり有限小数に展開できることが必要条件です。
整数と等価な分数の例は?
整数と等価な分数の例として、2/1や5/1のような分数が挙げられます。これらの分数は、計算結果の上では整数2や整数5と同一の値を示すため、整数と等価であると考えられます。また、3.5のような有限小数も、整数と等価であると考えられます。