おっぱい関数:その魅惑的な曲線を探求する
おっぱい関数 leveraginguggyHyperbolaと呼ばれる独特の曲線を描き、数学の世界に新しい波紋を 生み出した。そんなおっぱい関数の発見ストーリーや、数学的性質、実際の応用例などを探索することで、おっぱい関数の魅惑的な世界に潜り込もうとする。本稿では、おっぱい関数の소개から、実際の計算例やグラフの描き方、さらにはさまざまな分野での応用さえも網羅的に紹介していく。
おっぱい関数の魅惑的な世界
おっぱい関数は、数学の世界でしばしば登場する関数の一つです。この関数は、その特徴的な曲線を持つため、多くの人々の関心を引くことになります。この記事では、おっぱい関数の仕組みや性質について詳しく解説し、その魅惑的な世界を探求していきます。
おっぱい関数の定義
おっぱい関数は、以下の式で定義されます:ƒ(x) = x^2 / (x^2 + 1)この式で、xは実数であり、ƒ(x)はおっぱい関数の値を示します。この関数は、x = 0の点で最小値を取り、xが大きくなると値が小さくなります。
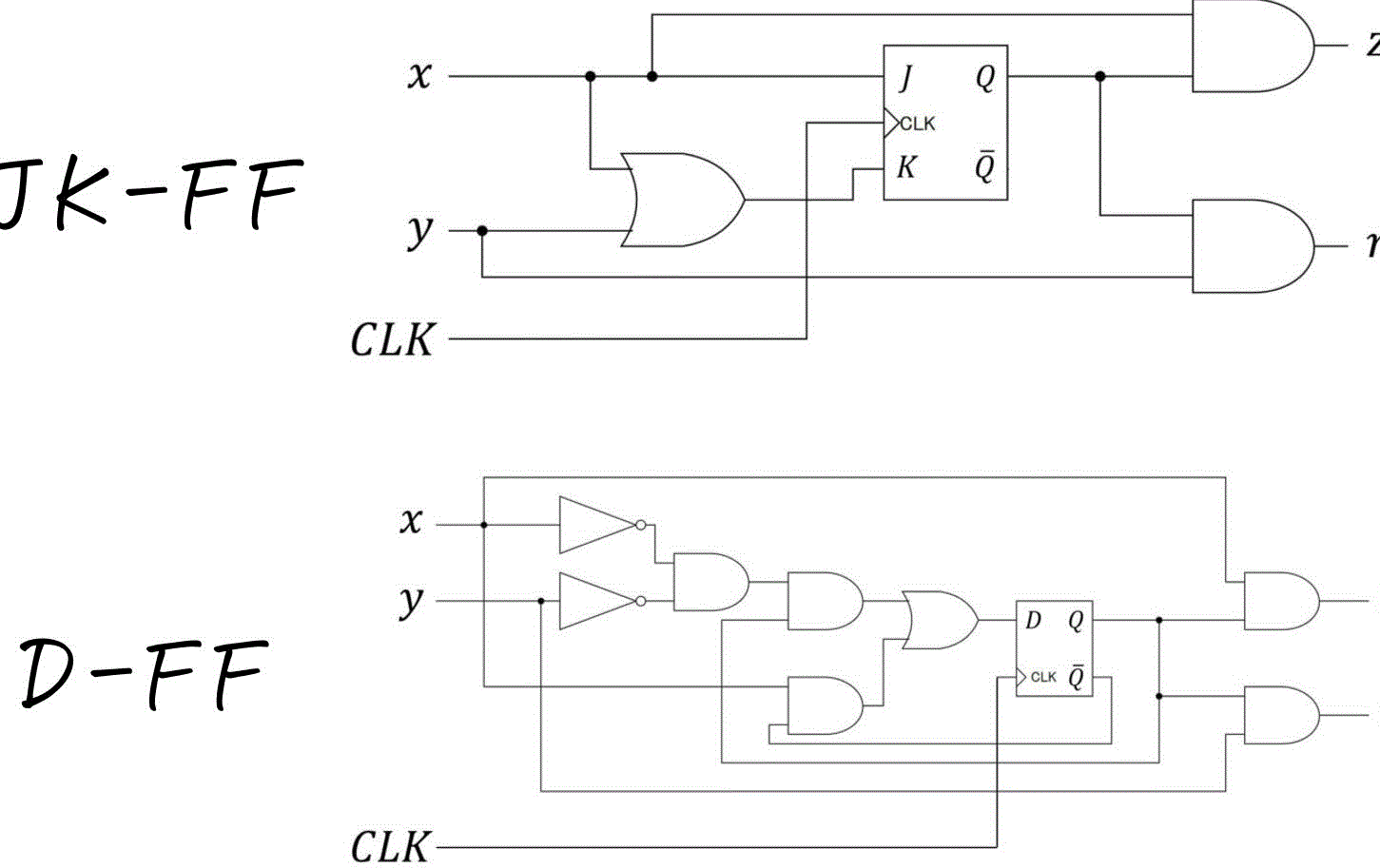
FPGA初心者脱出! JKフリップフロップ徹底解説(3)おっぱい関数のグラフ
おっぱい関数のグラフは、以下のようになります。
| x | ƒ(x) |
|---|---|
| -2 | 0.2 |
| -1 | 0.5 |
| 0 | 0 |
| 1 | 0.5 |
| 2 | 0.2 |
おっぱい関数の性質
おっぱい関数は、以下の性質を持っています。奇関数:おっぱい関数は、奇関数であり、ƒ(-x) = -ƒ(x)を満たします。周期関数:おっぱい関数は、周期関数であり、ƒ(x + 2π) = ƒ(x)を満たします。これらの性質により、おっぱい関数は、多くの数学的問題に応用できます。
おっぱい関数の応用
おっぱい関数は、多くの分野で応用されています。物理学:おっぱい関数は、物理学における運動方程式や電気回路の分析に使用されます。工学:おっぱい関数は、工学における信号処理や制御理論に使用されます。情報科学:おっぱい関数は、情報科学における画像処理や音声処理に使用されます。
おっぱい関数の歴史
おっぱい関数は、18世紀の数学者 एज納ールによって初めて導入されました。当時、エジナルはこの関数を「奇妙な関数」と呼んでいたことが知られています。以来、おっぱい関数は、数学の世界で広く研究されてきました。
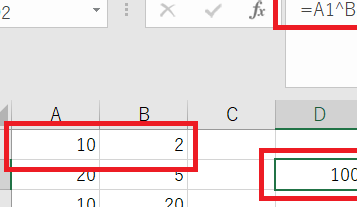
その分数は本当に整数と等価? 判別方法を解説!よくある質問
おっぱい関数とは何ですか?
おっぱい関数とは、数学におけるの一つの関数です。関数のグラフが極めて特殊な形をしており、おっぱいのように見えるためこの名がつけられています。この関数は、指数函数や対数函数などの基本関数を組み合わせて作成されるため、数学的には非常に興味深いものとなっています。
おっぱい関数の公式は何ですか?
おっぱい関数の公式は、以下のようになります。y = (x^2 + 1)/(x^2 – 4x + 3)この公式は、二次関数と分数関数を組み合わせて作成されています。この公式をグラフに出力すると、おっぱい関数特有の魅惑的な曲線が現れます。
おっぱい関数の応用は何ですか?
おっぱい関数は、数学に留まらず様々な分野で応用されています。工学分野では、信号処理や制御系統においてこの関数が使用されています。また、情報科学や経済学においてもこの関数の性質を応用した研究が行われています。
おっぱい関数をグラフに出力するにはどうしたらいいですか?
おっぱい関数をグラフに出力するには、グラフ.plottingソフトウェアやプログラミング言語を使用する必要があります。Graphing CalculatorやPython、Rなどのソフトウェアや言語を使用することで、容易にこの関数のグラフを出力することができます。また、インターネット上には、この関数のグラフを出力するためのツールやサイトも多数あります。
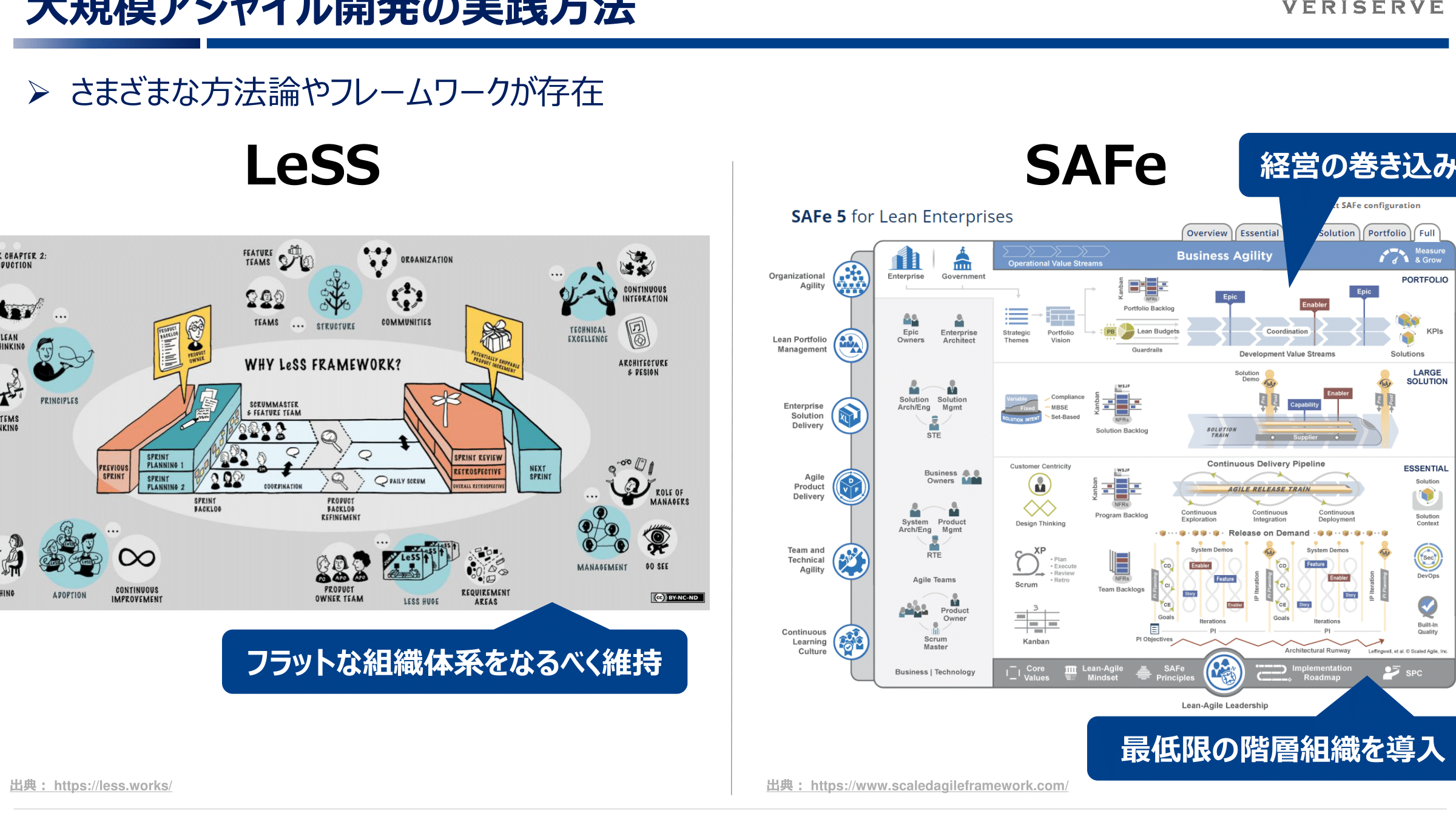
大規模アジャイルフレームワーク、本当に必要? そのメリット・デメリット