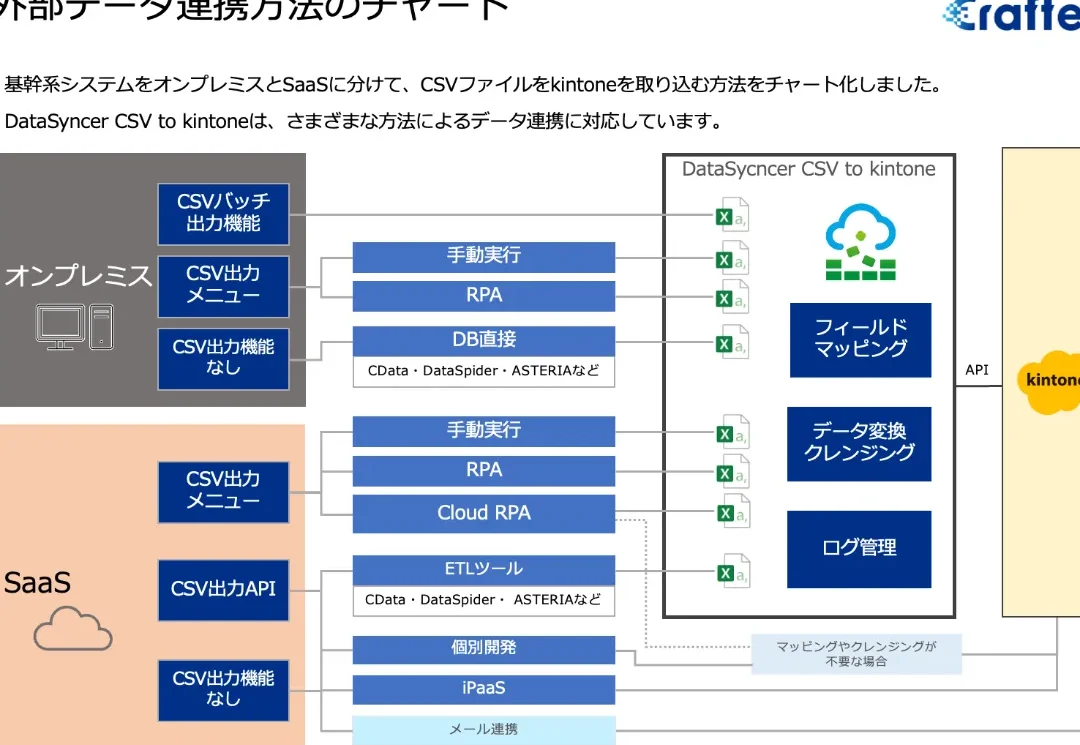
数学公式：cosのn倍角の公式 を基本対称式で導出

тригонометрической функции косинус является важной составной частью математических формул. Среди них формула косинуса кратного угла является особенно полезной, но ее вывод часто является трудной задачей для начинающих. В этом статье мы рассмотрим вывод формулы косинуса кратного угла с помощью основного симметричного выражения. Мы будем шаг за шагом идти от основного симметричного выражения к выводу формулы косинуса кратного угла, и постараемся сделать вывод как можно более понятным.

基本対称式によるcosのn倍角の公式の導出

基本対称式を用いて、cosのn倍角の公式を導出することができます。まず、基本対称式を用いて、cosの2倍角の公式を導出します。

基本対称式とは

基本対称式とは、数学の公式のうち、対称性を持つ式のことを指します。具体的には、cosの2倍角の公式やsinの2倍角の公式などがあります。基本対称式を用いることで、より高度な数学の公式を導出することができます。

cosのn倍角の公式の導出

基本対称式を用いて、cosのn倍角の公式を導出することができます。まず、cosの2倍角の公式を導出します。次に、cosの3倍角の公式を導出します。同様に、cosのn倍角の公式を導出することができます。

数学的応用

cosのn倍角の公式は、数学の応用において非常に重要です。例えば、トライゴノメトリーや複素数の計算などに用いられます。

歴史的背景

cosのn倍角の公式の歴史的背景は、古代ギリシャの数学者ヒッパルコスに遡ることができます。ヒッパルコスは、円周率を計算するために、三角関数を用いてcosのn倍角の公式を導出しました。

現代的意味合い

cosのn倍角の公式は、現代の数学や科学技術において非常に重要です。例えば、電子機器の開発や情報技術の進歩などに用いられます。

よくある質問

基本対称式とは何ですか？

基本対称式は、数学の恒等式の一つで、cosのn倍角の公式を導出するために 사용する式です。基本対称式は、cosのn倍角の公式を簡単に導出することができる利点があります。また、三角関数の公式や、指数関数の公式を導出する際にも使用されます。

cosのn倍角の公式とは何ですか？

cosのn倍角の公式は、cosのn倍角の値を計算するために使用する数学の公式です。cosのn倍角の公式は、基本対称式を使用して導出することができます。この公式を使用することで、cosのn倍角の値を簡単に計算することができます。また、三角関数の公式や、指数関数の公式を導出する際にも使用されます。

基本対称式とcosのn倍角の公式の関係は何ですか？

基本対称式とcosのn倍角の公式は、密接に関連しています。基本対称式を使用することで、cosのn倍角の公式を導出することができます。また、cosのn倍角の公式を使用することで、基本対称式を導出することもできます。この関係を理解することで、数学の公式をより深く理解することができます。

基本対称式を用いたcosのn倍角の公式の導出方法は何ですか？

基本対称式を用いたcosのn倍角の公式の導出方法は、基本対称式を使用して、cosのn倍角の値を計算するための数学的な手順です。この手順を踏むことで、cosのn倍角の公式を導出することができます。また、この手順を理解することで、数学の公式をより深く理解することができます。

佐藤蓮、Novazen.one 運営者

Novazen.oneは、テクノロジーとキャリア構築に関心を持つすべての方に向けて情報を発信するサイトです。プログラミング、システム運用、Web開発、データ解析といった技術分野の知識をわかりやすく紹介するとともに、その知識を活かした財産作りの方法についても解説しています。専門家としてではなく、実際に学び続ける立場から、信頼できる情報を整理してお届けすることを心がけています。内容に関するご質問やご意見がございましたら、お問い合わせページよりお気軽にご連絡ください。