数学の基礎を復習! 3点を通る平面の方程式 の求め方

数学の基礎を復習!高校生の数学では、三点を通る平面の方程式を求める問題が出題されることが多い。三角形の三頂点の座標が与えられたとき、平面の方程式を nasıl 求めるのか 는、数学の基礎的中間ضيでありながら、怪しく感じる生徒も多い。そんな中、本記事では、三点を通る平面の方程式を求める方法をわかりやすく解説することにした。
数学の基礎を復習! 3点を通る平面の方程式の求め方
数学の基礎を復習する上で、3点を通る平面の方程式の求め方は非常に重要です。この方法をマスターすることで、さまざまな数学の問題に挑戦することができます。
座標軸と平面の方程式
平面の方程式を求めるためには、座標軸の概念を理解する必要があります。座標軸とは、x軸、y軸、z軸の3つの軸で構成され、原点を中心として空間を捉えることを指します。座標軸を用いて、平面の方程式を表現することができます。
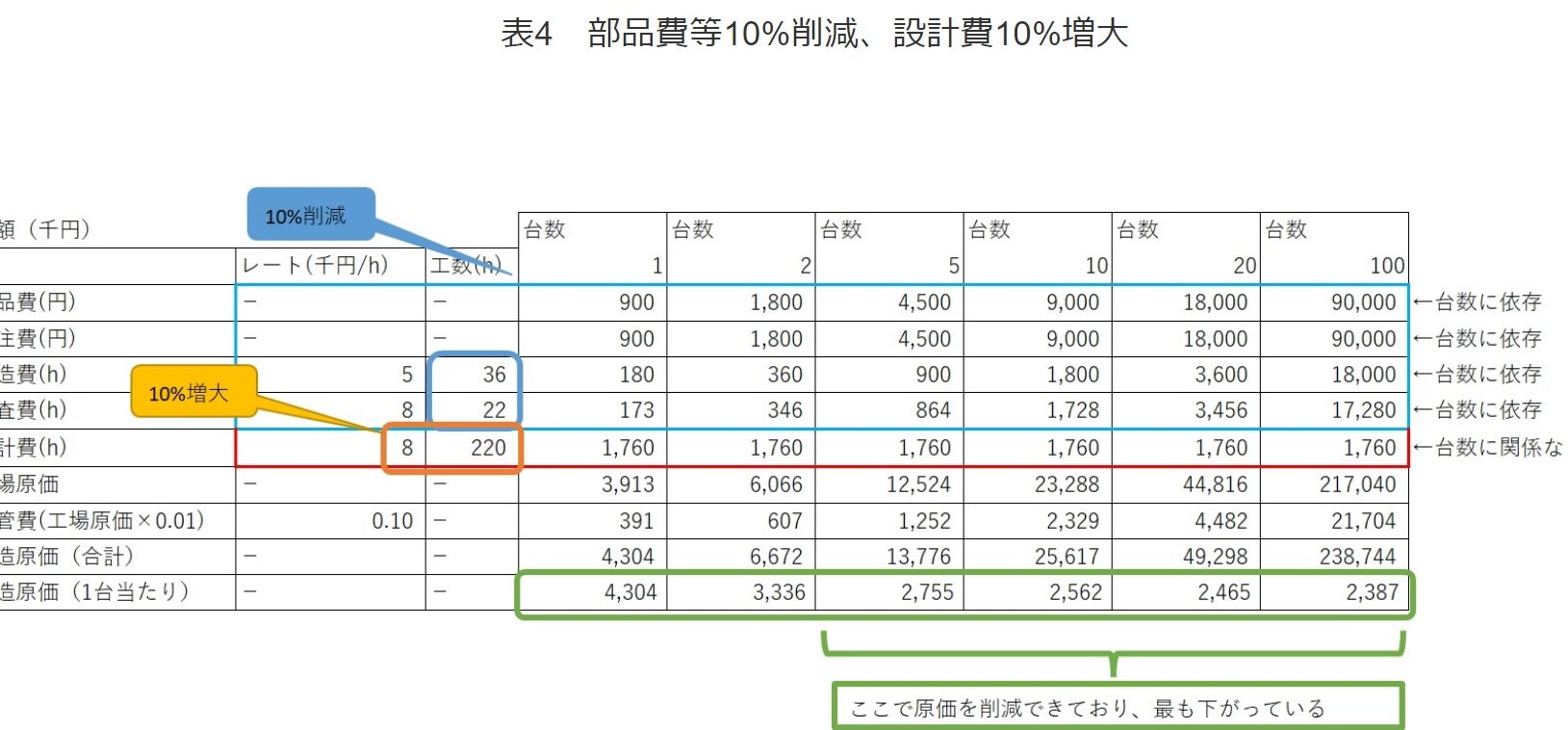
コスト削減の基礎知識:効果的なコストダウン手法を解説| 座標軸 | 説明 |
|---|---|
| x軸 | 水平方向の軸 |
| y軸 | 垂直方向の軸 |
| z軸 | 奥行き方向の軸 |
3点を通る平面の方程式の基本形
3点を通る平面の方程式の基本形は、次の式で表されます。Ax + By + Cz = Dこの式では、A、B、Cは平面の係数、x、y、zは座標、Dは定数です。
3点を指定することで平面の方程式を求める
3点を指定することで、平面の方程式を求めることができます。具体的には、3点の座標を用いて、平面の方程式を計算することができます。例えば、3点を(x1, y1, z1)、(x2, y2, z2)、(x3, y3, z3)とすると、平面の方程式は次のようになります。
平面の方程式を求めるための計算方法
平面の方程式を求めるためには、行列を用いて計算することができます。具体的には、3点の座標を用いて、行列を計算し、平面の方程式を求めることができます。
| 計算方法 | 説明 |
|---|---|
| 行列の計算 | 3点の座標を用いて、行列を計算する |
| 平面の方程式の求め方 | 行列の計算結果を用いて、平面の方程式を求める |
応用例:3点を通る平面の方程式の利用
3点を通る平面の方程式は、さまざまな数学的問題に応用することができます。例えば、立体幾何学や計算機グラフィックスでは、3点を通る平面の方程式を用いて、空間の形状を捉えることができます。
【アニメ制作】長編アニメーションを制作するためのノウハウを公開!三点平面の公式は?
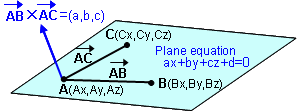
三点平面の公式は、三点を通る平面の一意な式を示すための数学公式です。三点平面の公式は、 Spiele rl式とも呼ばれます。
三点平面の公式の導出
三点平面の公式は、座標幾何学の基本的な概念に基づいて導出されます。まず、三点P、Q、Rの座標を(x₁,y₁,z₁)、(x₂,y₂,z₂)、(x₃,y₃,z₃)とします。次に、QPとPRの 벡터を求め、外積を計算します。最後に、求めた外積を normalize し、三点平面の公式を完成します。
三点平面の公式の応用
三点平面の公式は、コンピュータグラフィックスやロボット工学、CADなど、多くの分野で応用されています。
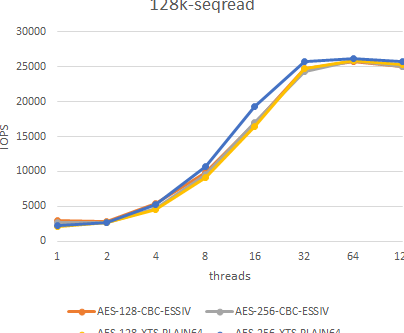
AES暗号化 速度対決! Raspberry Pi 3 vs PINE64 vs Intel VM- コンピュータグラフィックスでは、三点平面の公式を用いて、3Dモデルの表面を描画します。
- ロボット工学では、三点平面の公式を用いて、ロボットの運動計画を立てます。
- CADでは、三点平面の公式を用いて、設計図面を描画します。
三点平面の公式の注意点
三点平面の公式を使用する際には、以下の点に注意する必要があります。
- 三点が一直線上にある場合、三点平面の公式は不定義になります。
- 三点の座標が誤っている場合、三点平面の公式の結果も誤了します。
- 計算の丸め誤差も、三点平面の公式の結果に影響を与える可能性があります。
平面の方程式における法線ベクトルとは?

平面の方程式における法線ベクトルは、平面の.normal vector(法線ベクトル)を意味し、平面の法線方向を示すベクトルを指します。法線ベクトルの大きさは、平面上の任意の点における法線方向の長さを表します。
法線ベクトルの計算方法
法線ベクトルの計算方法はいくつかあります。
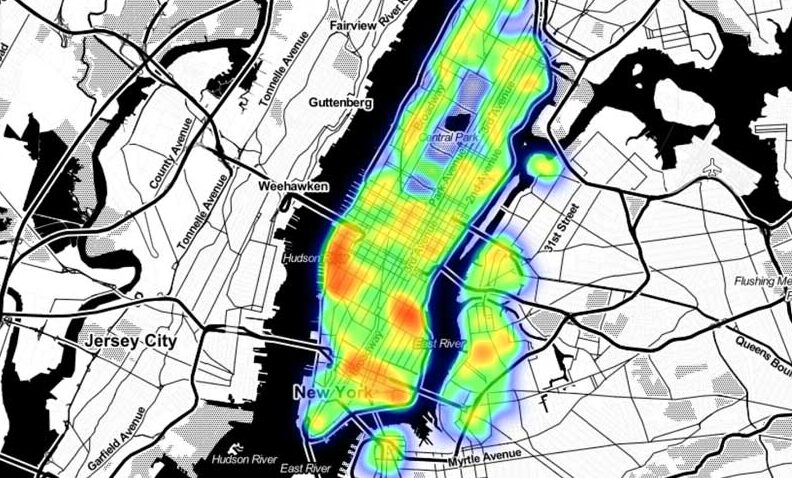
AI × 位置情報分析 でクレジットカード詐欺を撲滅!- 平面の方程式ax + by + cz = dを用いて、法線ベクトル(a, b, c)を計算する方法。
- 三点P1、P2、P3を用いて、平面を定義し、法線ベクトル(x2 – x1, y2 – y1, z2 – z1) × (x3 – x1, y3 – y1, z3 – z1)を計算する方法。
- 平面の方程式を代数的に処理し、法線ベクトル(∂f/∂x, ∂f/∂y, ∂f/∂z)を計算する方法。
法線ベクトルの用途
法線ベクトルは、平面上の幾何学的な問題には不可欠なものです。
- 平面上での距離や角度の計算に使用される。
- 平面上での投影や影の計算に使用される。
- コンピューターグラフィックスやゲーム開発における立体幾何学的な処理に使用される。
法線ベクトルの性質
法線ベクトルには、幾何学的な性質がいくつかあります。
- 法線ベクトルの大きさは、平面上の任意の点における法線方向の長さを表す。
- 法線ベクトルの向きは、平面の向きと一致する。
- 法線ベクトルの方向は、平面上での運動や変換に対して不変である。
数学で平面とは何ですか?

数学で平面とは、何ですか?
Amazonプライム ダウンロード機能徹底解説:制限と注意点平面は、数学における基本的な概念の一つです。特に、幾何学や図形学において wicht wichtigな役割を果たします。平面とは、自らが含まれない一点もない三次元空間内の二次元の面を指します。
平面の定義
平面の定義には、幾何学的および代数的な二つの方法があります。
- 幾何学的な定義:三次元空間内の二次元の面で、自らが含まれない一点もないというもの。
- 代数的な定義:三つの点を通る二次元の面で、座標系における式として表されるもの。
平面の性質
平面には、幾何学的な性質がいくつかあります。
- 平坦性:平面は、三次元空間内の二次元の面であるため、平坦な面をpossesses。
- 無限大:平面は、無限大に広がる二次元の面である。
- 平行性:平面同士が、平行関係にある。
平面の応用
平面の概念は、数学や物理学、工学など、広範囲にわたって応用されます。
- 幾何学:平面は、幾何学における基本的な概念である。
- 物理学:平面は、物理学における力学や運動の理論において重要な役割を果たす。
- 工学:平面は、工学における設計や製造において重要な概念である。
平面の法線とは?

平面の法線とは、ある平面上において、該当平面に対して垂直な方向を指します。すなわち、平面と垂直な線であることを意味します。この法線は、幾何学や物理学、コンピュータグラフィックスなど様々な分野で重要な概念です。
平面の法線の特徴
平面の法線には、以下のような特徴があります。
- 垂直性:平面と垂直な方向を指します。
- 一意性:ある平面に対して、唯一の法線が存在します。
- 向き付け:法線には向き付けがあり、平面に対する向きを示します。
平面の法線の計算方法
平面の法線を計算する方法はいくつかあります。以下は、一般的な方法の1つです。
- 三つの点を指定し、平面を定義します。
- これらの三点を通るベクトルを計算し、法線ベクトルを得ます。
- 法線ベクトルの正規化を行い、単位ベクトルとしての法線を得ます。
平面の法線の応用
平面の法線は、以下のような分野で応用されます。
- 物理学:力学や電磁気学で、平面に対する力や電磁気の方向を計算するために使用します。
- コンピュータグラフィックス:3Dグラフィックスの描画や、光源のシミュレーションに使用します。
- 機械工学:機械の設計や、運動のシミュレーションに使用します。
よくある質問
平面の方程式を求めるために必要な数学の基礎は何か?
平面の方程式を求めるためには、三角関数や高次方程式、座標幾何などの数学の基礎知識が必要です。特に、三角関数の理解が不足している場合、平面の方程式を求めることができません。また、高次方程式の解法についても心得ている必要があります。
3点を通る平面の方程式を求めるための公式は?
3点を通る平面の方程式を求めるための公式は、三点形式という式を使います。この式では、三つの点の座標を用いて平面の方程式を求めることができます。ただし、この式を正しく適用するためには、数学の基礎知識が必要です。
平面の方程式を求める際に注意すべき点は何か?
平面の方程式を求める際には、点の座標や計算の順序に注意する必要があります。まず、三つの点の座標を正しく設定する必要があります。次に、計算の順序を間違えないように注意する必要があります。あらかじめ、計算の順序を確認しておくことが大切です。
平面の方程式を実際の問題に適用するにはどうしたらよい?
平面の方程式を実際の問題に適用するには、問題の理解や式の適用が大切です。まず、問題の内容を正しく理解する必要があります。次に、平面の方程式を適用する際には、数学の基礎知識を思い出して、正しく式を適用する必要があります。