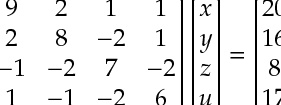
ツリーの重心分解(木の重心分解)を図解！ アルゴリズムを理解

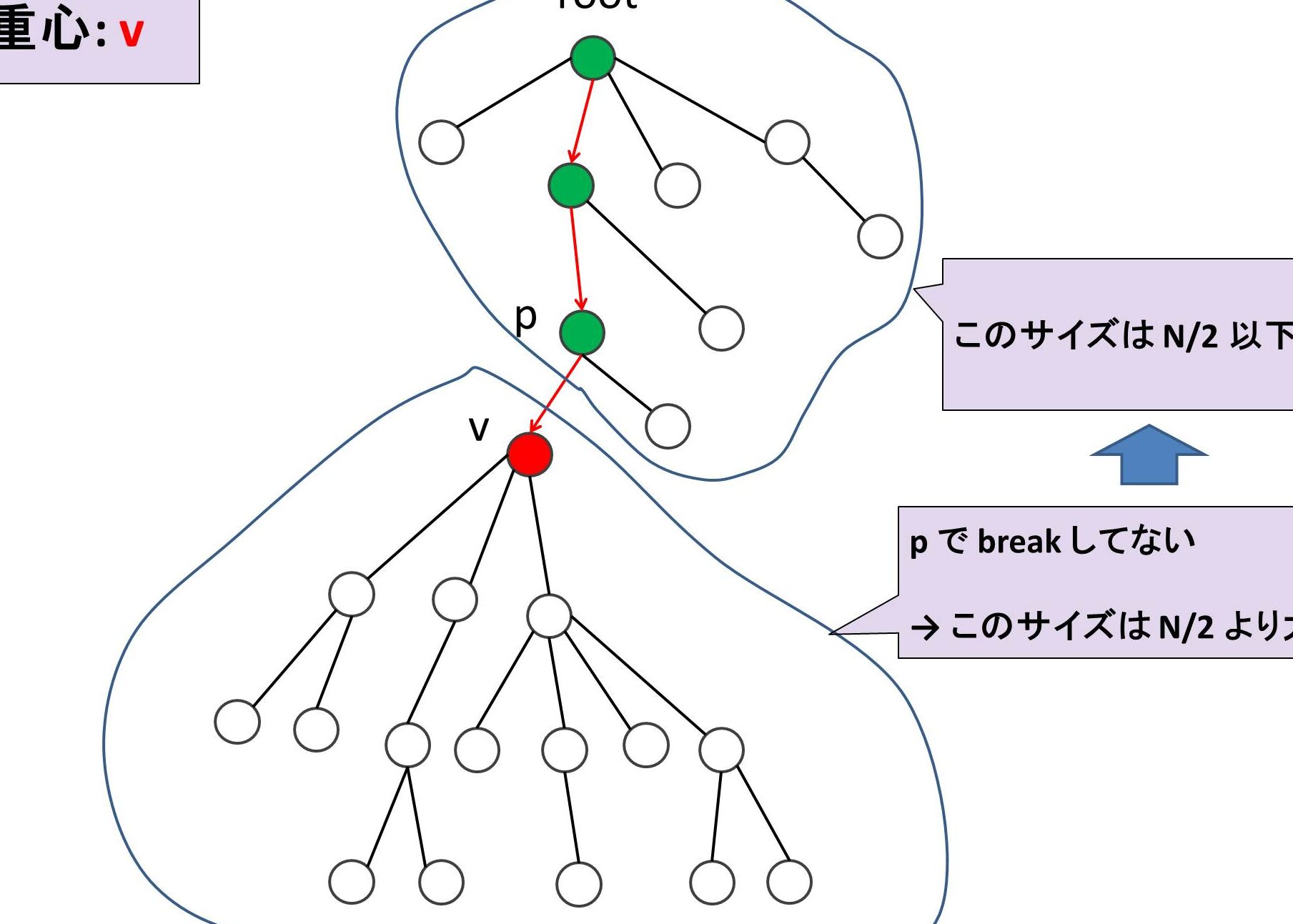
木の重心分解は、グラフ理論における重要な概念の一つです。木構造を分解し、各部分木の重心を求めることで、様々な応用が可能になります。しかし、木の重心分解のアルゴリズムを理解することは、初学者にとってはやや難しいと感じられます。本稿では、木の重心分解のアルゴリズムを図解によってわかりやすく解説し、読者の理解を深めることを目的としています。

ツリーの重心分解を.step by step図解！ アルゴリズムを理解するためのコツ

ツリーの重心分解は、木の構造を分析する上で非常に重要な概念です。このアルゴリズムを理解することで、木の構造をより深く理解し、様々な問題を解くことができます。

ツリーの重心分解の定義

ツリーの重心分解とは、木の構造を分解し、中心的なノードを特定する手法です。このアルゴリズムを使用することで、木の中心的な部分を特定し、木の構造をよりわかりやすくすることができます。重心という言葉は、木の中心点にあるノードを指します。

ツリーの重心分解のアルゴリズム

ツリーの重心分解のアルゴリズムは、以下の手順で実行されます。

ツリーの重心分解の利点

ツリーの重心分解には、以下のような利点があります。

• 木の構造をわかりやすくする
• 中心的なノードを特定する
• 木の各ノードの次数を計算する
• 木の最小コストを計算する

ツリーの重心分解のアプリケーション

ツリーの重心分解は、以下のようなアプリケーションに使用されます。

• ネットワークの最適化
• クラスタリング分析
• 木の構造を分析するための基礎理論
• 計算機科学の基礎理論

ツリーの重心分解の展望

ツリーの重心分解の将来の展望として、以下のような方向性があります。

• より高速なアルゴリズムの開発
• 木の構造のより詳細な分析
• ネットワーク科学の応用
• 計算機科学の進歩

よくある質問

ツリーの重心分解とは何ですか?

ツリーの重心分解は、木の構造を分解して、重心という概念を用いて、木の中心的なノードを特定するアルゴリズムです。このアルゴリズムを用いることで、木の構造をわかりやすく分解することができ、計算効率をアップさせることができます。木の重心分解は、グラフ理論の分野では非常に重要な概念であり、多くのアルゴリズムで使用されています。

ツリーの重心分解のアルゴリズムはどのように動作しますか?

ツリーの重心分解のアルゴリズムは、まず木の構造を探索し、ノードの次数を計算します。次に、次数が低いノードを中心として、木の構造を分解します。この過程で、木の中心を特定し、重心を計算します。最後に、木の構造を分解することで、計算効率をアップさせることができます。

ツリーの重心分解の利点とは何ですか?

ツリーの重心分解の利点は、計算効率が高まることです。木の構造を分解することで、計算時間を短縮することができます。また、木の中心を特定することで、木の構造をわかりやすく分解することができます。さらに、グラフ理論の分野では、多くのアルゴリズムで使用されるため、汎用性が高まります。

ツリーの重心分解をどこで使用するのですか?

ツリーの重心分解は、グラフ理論の分野で広く使用されています。特に、最短経路問題や、最小スパニングツリー問題などの問題を解くために使用されます。また、コンピューターネットワークの分野では、ネットワークの構造を最適化するために使用されます。さらに、データマイニングの分野では、データの構造を分析するために使用されます。

レン、「技術分野における最高のガイド」の創設者です。

私は職業としてのエンジニアではありませんが、情熱としてのエンジニアです。技術分野における最高のガイドを立ち上げたのは、デジタル世界のあらゆる知識やリソースを紹介するためです。すべてをよりシンプルで理解しやすい視点から誰にでも伝えられるよう心がけています。

MATLAB S-Function Builderの使い方 – Arduino連携ライブラリ自作