「計算力学 有限要素法の基礎」 自分まとめ!

計算力学における有限要素法は、 громledgeの基礎的技術です。物質の変形や応力の分布を予測することで、製品開発やインフラ整備に大きく寄与します。しかし、有限要素法の理論や手法は複雑で、学習の敷居が高く感じる人も多いでしょう。本記事では、有限要素法の基礎についてわかりやすくまとめ、計算-powerの励みとなることを目指します。自分自身の理解を深めるためのまとめでありながら、シリーズではじめの一歩を踏み出します。
「計算力学 有限要素法の基礎」自体まとめ!
計算力学有限要素法は、構造物や機械の強度、剛性、歪みなどの物理的な挙動を予測し、設計や解析を行うための数値解析手法です。この手法は、実際の問題を離散化し、有限要素に分割して計算を行うことで、複雑な物理現象を解析することができます。
有限要素法の基本的な考え方
有限要素法は、実際の問題を離散化し、有限要素に分割して計算を行うことで、複雑な物理現象を解析することを目指しています。この手法では、問題領域を小さい要素に分割し、それぞれの要素での物理量を計算し、全体の挙動を予測することができます。有限要素とは、実際の問題を小さい要素に分割したものであり、各要素での物理量を計算することで、全体の挙動を予測することができます。
電験3種 わかりにくい箇所の解説! 資格取得をサポート!有限要素法の種類
有限要素法には、幾何学的有限要素法、ophysical有限要素法、混合有限要素法などの種類があります。幾何学的有限要素法は、幾何学的な形状に基づいて有限要素を設定することで、構造物や機械の強度や剛性を予測することができます。ophysical有限要素法は、物理的な現象に基づいて有限要素を設定することで、熱伝導や流体力学などの現象を予測することができます。
有限要素法の利点
有限要素法には、以下のような利点があります。高精度:有限要素法を使用することで、高度な精度で物理現象を予測することができます。柔軟性:有限要素法を使用することで、複雑な物理現象を解析することができます。計算速度:有限要素法を使用することで、計算速度を向上させることができます。
有限要素法の適用例
有限要素法は、以下のような分野に適用されています。構造物の設計:有限要素法を使用することで、構造物の強度や刚性を予測し、設計を行うことができます。機械の設計:有限要素法を使用することで、機械の動作や性能を予測し、設計を行うことができます。医療機器の開発:有限要素法を使用することで、医療機器の性能や安全性を予測し、開発を行うことができます。
有限要素法の将来展望
有限要素法の将来展望は、以下のようなものです。高性能計算の発展:高性能計算技術の発展によって、有限要素法の計算速度を向上させることができます。多物理場有限要素法:多物理場有限要素法の開発によって、複雑な物理現象を更に正確に予測することができます。
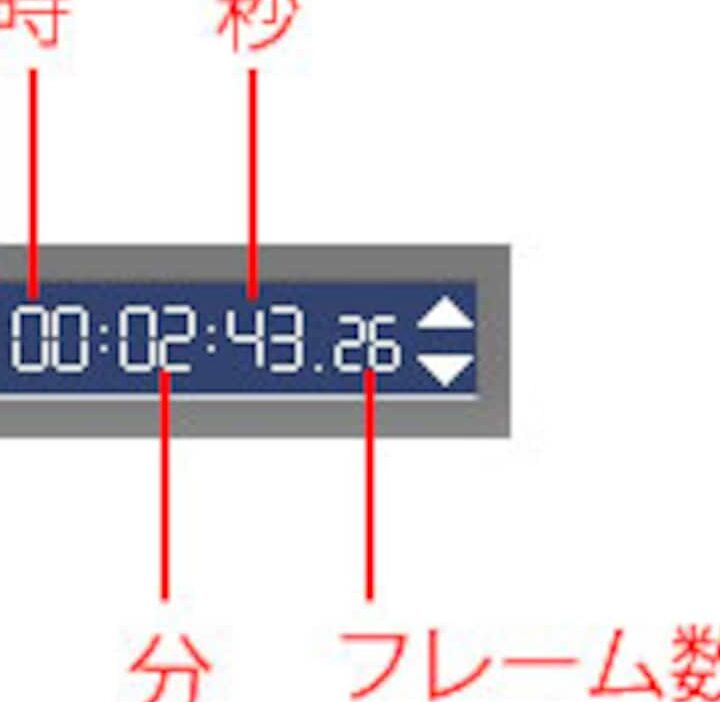
映像制作の基礎知識!フレームレート、タイムコード、タイムスタンプ!| 有限要素法 | 利点 | 適用例 |
|---|---|---|
| 幾何学的有限要素法 | 高精度、柔軟性 | 構造物の設計 |
| ophysical有限要素法 | 高精度、柔軟性 | 熱伝導、流体力学 |
| 混合有限要素法 | 高精度、柔軟性 | 複雑な物理現象 |
有限要素法の計算手順は?
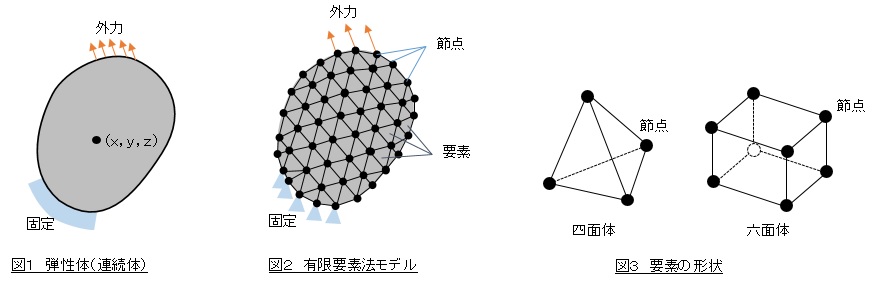
有限要素法の計算手順は、以下のようになります。
前処理
有限要素法の計算の前には、問題設定、メッシュ生成、要素の性質設定などの前処理が必要です。特に、メッシュ生成では、計算領域を細かく分割することで、計算の精度を高めることができます。
- 問題設定:計算対象の問題を設定し、計算の目的を明確化する。
- メッシュ生成:計算領域を細かく分割して要素を作成する。
- 要素の性質設定:要素の性質、例えば材料の物理的性質を設定する。
解析
有限要素法の計算の本体では、ガルキン法やニュートン法などの数値解析技法を用いて、微分方程式を解きます。このステップでは、連立方程式を解くために、 반복計算を繰り返します。
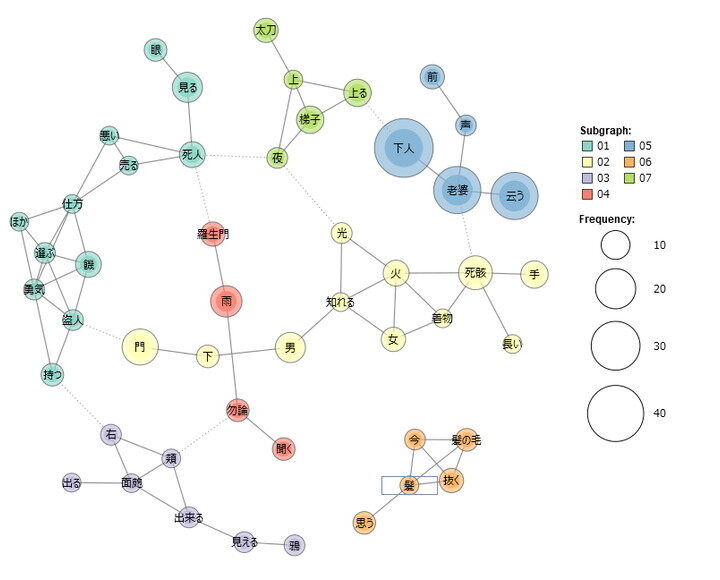
データ分析で関係性を可視化!クラスター分析と共起ネットワーク描画入門- 微分方程式の設定:計算対象の微分方程式を設定する。
- 数値解析技法の選択:ガルキン法、ニュートン法などの数値解析技法を選択する。
- 連立方程式の解析:連立方程式を解くために、反復計算を繰り返す。
後処理
有限要素法の計算の後には、結果の評価や可視化を行います。このステップでは、計算結果をもとに、応力や変形などの物理量を計算し、可視化します。
- 結果の評価:計算結果を評価し、誤差を計算する。
- 可視化:計算結果を可視化し、物理量を表現する。
- 物理量の計算:応力や変形などの物理量を計算する。
有限要素法はどのような分野で用いられますか?

有限要素法は、数値解析やシミュレーションにおいて、様々な分野で広く用いられています。特に、構造解析や熱伝導解析、Fluid Dynamicsなどの分野で利用されています。
構造解析
有限要素法を用いた構造解析では、構造物の強度や剛性を解析するために使用されます。この方法により、応力分布や歪み分布を計算することができます。特に、橋梁や高層ビル、機械部品などの構造物の設計や解析に用いられています。
コインパーキング料金の謎を解明!複雑な料金体系を完全理解!- 構造物の強度解析
- 剛性解析
- 応力分布や歪み分布の計算
熱伝導解析
有限要素法を用いた熱伝導解析では、熱伝導率や温度分布を計算するために使用されます。この方法により、電子機器や自動車、建築物などの熱設計や解析に用いられています。
- 熱伝導率の計算
- 温度分布の計算
- 熱設計や解析
Fluid Dynamics
有限要素法を用いたFluid Dynamicsでは、流体の運動や圧力分布を計算するために使用されます。この方法により、航空機や自動車、造船などの fluid dynamics 関連分野での設計や解析に用いられています。
- 流体の運動の計算
- 圧力分布の計算
- fluid dynamics 関連分野での設計や解析
FEMとはどういう意味ですか?
FEMとは、Finite Element Methodの略称です。これは、数値解析手法の一つで、微分方程式や積分方程式を数値的に解くために用いられます。有限要素法と呼ばれるこの手法は、複雑な幾何形状や非線形の問題でも高い精度で解析結果を得ることができます。
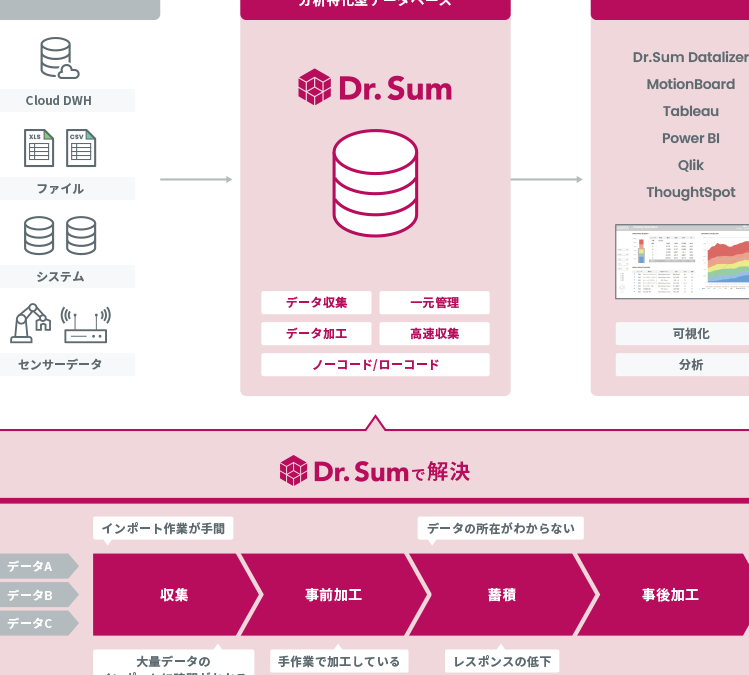
Tableauの代わりにDr.Sumでデータ分析!データベース活用術FEMの基本的なSteps
この手法では、以下のstepを踏みながら解析を実施します。
- 問題設定:対象とする問題の設定を行います。
- 網掛け:対象とする領域を小さな要素に分割し、網掛けを実施します。
- 數値計算:網掛けされた要素ごとに、数値計算を実施します。
FEMの特徴
Finite Element Methodには、以下のような特徴があります。
- 幾何形状の自由度:複雑な幾何形状の問題でも高い精度で解析結果を得ることができます。
- 非線形の問題に対する適用:非線形の問題でもFINITE ELEMENT METHODが有効に働きます。
- 高精度な解析結果:数値計算により高い精度の解析結果を得ることができます。
FEMの適用分野
FINITE ELEMENT METHODは、広範囲な分野に適用されます。
- 構造解析:建築物、橋梁、機械構造物などの構造解析に用いられます。
- 熱伝導解析:熱伝導率の計算、熱ストレスの解析などに用いられます。
- 流体力学:流体の運動をシミュレートし、流体力学的現象を研究します。
有限体積法と有限要素法の違いは何ですか?
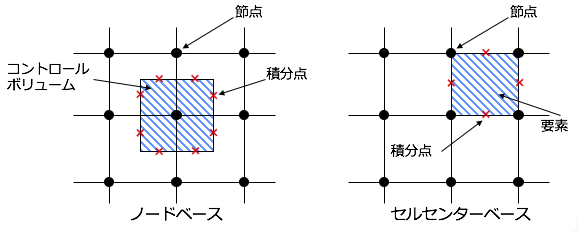
計算手法の違い
有限体積法と有限要素法の計算手法が異なる点は、有限体積法がROADCASTの手法に基づいており、有限要素法はGalerkinの手法に基づいていることである。有限体積法では、領域を小さな体積要素に分割し、各要素の物理量を計算する。一方、有限要素法では、領域を小さな要素に分割し、各要素の境界で物理量を計算する。
適用領域の違い
有限体積法と有限要素法の適用領域も異なる。有限体積法は、流体力学や熱伝導などの問題に適しており、有限要素法は、固体力学や構造解析などの問題に適している。また、有限体積法は、非線形の問題に適しており、有限要素法は、線形の問題に適している。
- 流体力学:有限体積法
- 固体力学:有限要素法
- 熱伝導:有限体積法
計算精度の違い
有限体積法と有限要素法の計算精度も異なる。有限体積法は、遅れ中心差分法やUpwind法を使用することで高い計算精度を実現できる。一方、有限要素法は、Galerkinの手法を使用することで高い計算精度を実現できる。また、有限体積法は、大規模な問題に適しており、有限要素法は、小規模な問題に適している。
- 遅れ中心差分法:有限体積法
- Upwind法:有限体積法
- Galerkinの手法:有限要素法
よくある質問
有限要素法の基礎とは何ですか?
有限要素法の基礎とは、計算力学の分野において、構造物や流体の挙動を解析するための数値解析手法の一つです。有限要素法は、問題領域を小さな要素に分割し、各要素における関数の近似値を計算することで、問題全体の解を近似的に導き出すことができます。基礎という言葉が含まれているため、計算力学の基礎的な理論や原理に焦点を当てた内容を指します。
計算力学の適用領域はどこですか?
計算力学は、非常に広い範囲の分野に適用可能です。構造力学、Fluid Dynamics、熱伝導、電磁気学など、様々な分野での問題解析に使用できます。有限要素法やBoundary Element Methodなどの数値解析手法を組み合わせることで、 càngも複雑な問題を解析することができます。
自己まとめの重要性はどこにあるのですか?
自己まとめは、計算力学の学習や研究において非常に重要な要素です。基礎理論や数値解析手法など、計算力学に関する様々な概念や技術を体系的に整理し、自分の頭の中にまとめることで、より深く理解し、応用することができます。自己まとめを行うことで、計算力学に関する問題に対する思考力や解析能力を向上させることができます。
計算力学の将来的な展望は何ですか?
計算力学の将来的な展望は、非常に明るいです。AIやMachine Learningなどの新しい技術と組み合わせることで、計算力学はますます発展し、より高度な問題を解析することができます。多物理現象シミュレーションや逆問題解析などの新しいアプローチも登場しており、計算力学はますます幅広い分野での応用が期待されます。